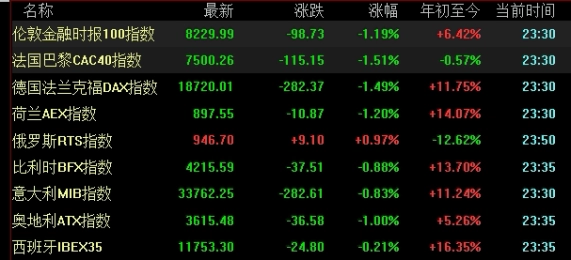
脑洞大开!期权定价模型(发展历程、主要模型、应用实例以及未来趋势)
期权定价模型是金融工程领域的核心内容之一,它为理解和评估期权价值提供了理论基础和计算方法。将深入探讨期权定价模型的基本概念、发展历程、主要模型、应用实例以及未来趋势,旨在为读者提供一个全面而深入的视角。
什么是期权定价模型?
期权定价模型是用于估算期权理论价值的数学模型或框架。期权是一种衍生金融工具,赋予持有者在未来某一特定时间以特定价格买入或卖出某种资产的权利,而非义务。期权定价模型通过考虑多种因素,如标的资产的价格、执行价格、到期时间、无风险利率以及波动率等,来计算期权的公允市场价值。
期权定价模型的发展历程
期权定价模型的发展可追溯到20世纪初,但真正的突破发生在1973年,当Black和Scholes提出了他们的革命性模型——Black-Scholes模型。这一模型基于几个关键假设,包括市场无摩擦、资产价格遵循几何布朗运动、无风险利率恒定等,为欧式期权的定价提供了精确的解析解。随后,Merton对Black-Scholes模型进行了扩展,考虑了股息支付的影响,形成了Black-Scholes-Merton模型。
主要的期权定价模型
Black-Scholes模型
如前所述,Black-Scholes模型是期权定价领域的基石,适用于无股息股票的欧式看涨和看跌期权。该模型通过五个输入参数(标的资产价格、执行价格、到期时间、无风险利率和波动率)来计算期权的理论价值。
Black-Scholes-Merton模型
Black-Scholes-Merton模型在Black-Scholes模型的基础上,增加了股息收益率作为第六个输入参数,使得模型能够更准确地反映支付股息的股票期权价值。
二叉树模型
二叉树模型是一种数值方法,用于处理更复杂的期权定价问题,特别是美式期权和路径依赖期权。该模型通过构建一个二叉树来模拟标的资产价格的所有可能路径,并使用动态规划技术反向求解期权价值。
Monte Carlo模拟
Monte Carlo模拟是另一种强大的数值方法,特别适用于处理高维或复杂路径依赖的期权定价问题。通过随机抽样模拟标的资产价格的大量可能路径,并计算这些路径下期权的平均收益,从而估计期权的价值。
期权定价模型的应用实例
期权定价模型广泛应用于金融市场的多个方面,包括但不限于:
- >风险管理:企业和金融机构利用期权定价模型对冲风险,优化投资组合。
- >投资策略:投资者根据期权定价模型制定交易策略,如套利、投机或保护性买入。
- >产品设计:金融机构设计新型金融产品时,依赖期权定价模型进行估值和定价。
- >监管合规:监管机构使用期权定价模型评估金融机构的市场风险暴露,确保市场稳定。
期权定价模型的未来趋势
随着金融科技的快速发展,期权定价模型也在不断进化。以下是一些可能的未来趋势:
- >机器学习与人工智能:结合机器学习算法,提高期权定价的准确性和效率。
- >高频数据与实时定价:利用高频数据进行实时期权定价,满足快速变化的市场需求。
- >复杂衍生品定价:开发新的模型和方法,以应对日益复杂的衍生品结构和市场环境。
- >全球市场整合:随着全球金融市场的进一步融合,跨市场、跨资产类别的期权定价模型将更加重要。
期权定价模型是连接理论与实践的桥梁,它们不仅为金融市场参与者提供了重要的决策工具,也推动了金融理论的发展。从Black-Scholes模型的提出到现代数值方法和机器学习技术的应用,期权定价模型不断演进,以适应日益复杂和多变的市场环境。未来,随着技术的不断进步和市场需求的持续变化,期权定价模型将继续发挥其在金融工程领域的核心作用,为全球金融市场的稳定和发展贡献力量。